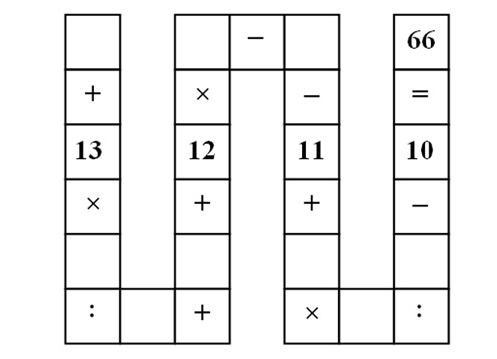
The Answer to the Third-Grade Math Problem from Vietnam that has Stumped Millions
In the diagram, the blanks must be filled with any number between 1 and 9 so that the equation works. Each number can only be used once. The colon “:” means divide. (check out the answer)
Here’s how Alex Bellos of the Guardian, a newspaper in the United Kingdom, explains it in his May 21, 2015 column, “Alex Bellos’s Adventures in Numberland:”
Rewrite the snake as an equation:
a + (13b/c) + d + 12e – f – 11 + (gh/i)– 10 = 66
We are trying to find a, b, c, d, e, f, g, h and i, which we know are some combination of the digits 1,2,3,4,5,6,7,8 and 9.
Before we even look for a solution, consider the total number of ways we could fill in the snake: there are 362,880 possible combinations of the digits 1 to 9 placed in nine slots.
We can tidy the equation to:
a + (13b/c) + d + 12e – f +(gh/i) = 66 + 11 + 10 = 87
or
a + d – f + (13b/c) + 12e +(gh/i) = 87
From here we can assume that b/c and gh/i will be whole numbers, and also that we don’t want 13b/c to be too big.
Knowing this, we start plugging numbers in and seeing where we get to.
There is more than one solution, so there are many difference guesses that will lead to the right number. (I didn’t write a program, but many of you did and from the comments it would seem that there are well over 100 solutions.)
The most intuitive answer offered yesterday I thought belonged to the contributor Brollachain. To keep the term 13b/c as small as we can, he let b = 2 and c = 1.
Which gets us to
a + d – f + 26 + 12e +(gh/i) = 87
or
a + d – f + 12e +(gh/i) = 61
The numbers remaining are the digits from 3 to 9. They include the prime numbers 3, 5 and 7. As Brollachain recommends, lets get rid of them asap so they don’t complicate the other terms.
Let a = 3, d = 5 and f = 7.
Which leaves us with
3 + 5 – 7 + 12e +(gh/i) = 61
or
12e +(gh/i) = 60
The numbers remaining are 4,6,8,9.
Playing around with these gets us
e = 4
g = 9
h = 8
i = 6
48 + (72/6) = 48 +12 = 60
There are some puzzles that you solve with a flash of insight, and some others – like this one – where there is no alternative but trial and error.
Both kinds can be very satisfying to solve.